3.4 The Topology of the Configuration Space

Topology is a branch of mathematics that considers properties of objects that do not change when the objects are subjected to arbitrary transformations such as stretching or bending. The classic example is that a coffee mug and a donut are topologically equivalent. Two spaces are topologically different if cutting or pasting is required to turn one into another.

For example, a circular mobile robot (${\mathbb{R}}^2$) and the two-joint planar arm ($T^2$) are topologically different. If we imagine $T^2$ as the surface of a donut, no amount of stretching will make the donut not have a hole in it (the area of the workspace where the robot would necessarily self-collide).

We care about the topology of configuration space because it allows us to utilize path planning techniques used in one configuration space across all topologically equivalent configuration spaces.

3.4.1 Homeomorphisms and Diffeomorphisms

A mapping $\varphi :S\to T$ is a rule that places elements of $S$ into correspondence with elements of $T$.

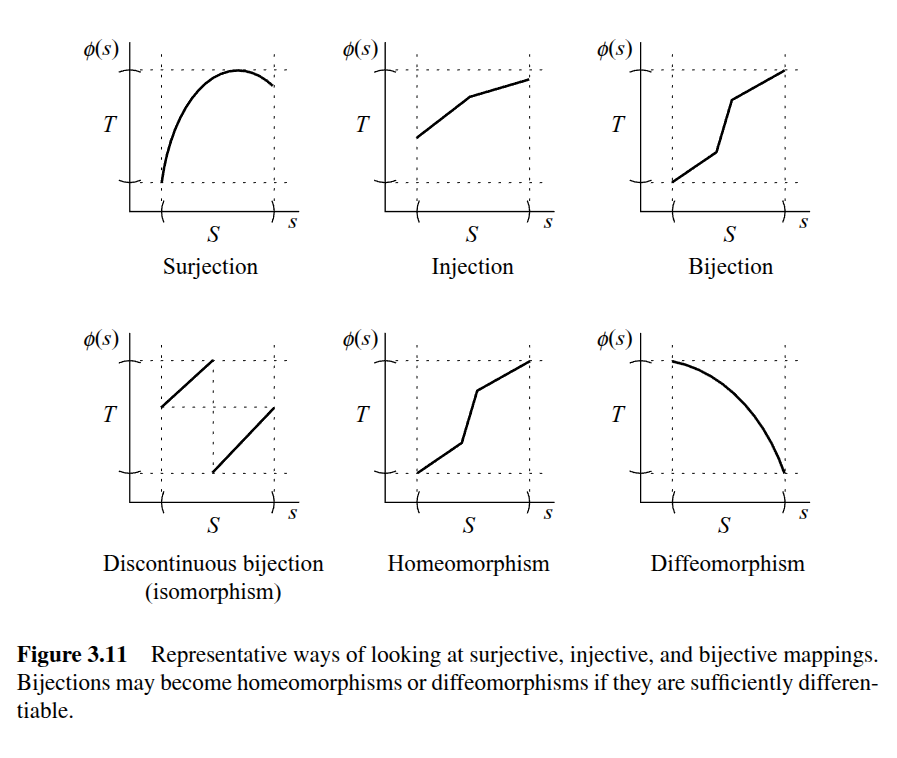
Types of mappings:

• Surjective or Onto
  • every element of $T$ is covered
• Injection
  • every element of $T$ is in correspondence with at most one element of $S$ (one-to-one)
• Bijection
  • every element of $T$ is in correspondence with one and only one element of $S$.
  • Mappings that are surjective and injective are Bijective.
  • Has the property that the inverse exists at every point in $T$

Classes of Bijective mappings:

• Homeomorphic
  • a mapping is homeomorphic if the mapping is bijective and the function and its inverse are continuous
• Diffeomorphic
  • When a mapping is homeomorphic and the mapping is smooth
  • a mapping is smooth if all partial derivatives of the mapping, of all orders, are well defined.

3.4.2 Differentiable Manifolds

We can uniquely specify a configuration by $n$ parameters, where $n$ is the dimension of the configuration space. We can do this because the configuration spaces were all “locally like” $n$-dimensional Euclidean spaces. These spaces are called “manifolds”.

Definition - Manifold: A set $S$ is a $k$-dimensional manifold if it is locally homeomorphic to ${\mathbb{R}}^k$, meaning that each point in $S$ possesses a neighborhood that is homeomorphic to an open set in ${\mathbb{R}}^k$.

While a general $k$-dimensional manifold is locally homeomorphic to ${\mathbb{R}}^k$, the configuration spaces we will consider are locally diffeomorphic to ${\mathbb{R}}^k$.

A differentiable manifold is a set of diffeomorphisms that are “compatible” with one another and that the set of diffeomorphisms covers every configuration in $Q$ in their domains.

Definition - Chart: A pair ($U,\varphi$), such that $U$ is an open set in a $k$-dimensional manifold and $\varphi$ is a diffeomorphism from $U$ to some open set in ${\mathbb{R}}^k$, is called a chart.

The subset $U$ is charted onto ${\mathbb{R}}^k$.

The inverse diffeomorphism is referred to as a parameterization of the manifold.

Consider the one-dimensional manifold of a circle in ${\mathbb{R}}^2$ with radius 1 centered at the origin called $S^1$. For any point we can define a neighborhood that is diffeomorphic to $\mathbb{R}$. For instance, consider the upper half of the circle. Taking just the x coordinate of each point is a diffeomorphism to $\mathbb{R}$. $U_1=x\in S^1|x_2>0,{\varphi }_1(x)=x_1$ Yet the circle is not totally diffeomorphic to $\mathbb{R}$, and never can be. There is not a single chart whose domain includes all of $S^1$.

When we represented the 2 link planar arm in 3.1 Specifying a Robot’s Configuration as (${\theta }_1,{\theta }_2$) we were in fact creating a chart from a subset of the configuration space (which is a manifold) to ${\mathbb{R}}^2$. A single mapping from $T^2$ to ${\mathbb{R}}^2$ encounters continuity problems at the bounds ({0, $2\pi$}).

Constructing a single chart to cover the configuration space will become infeasible. In this case we will construct a collection of charts. We cannot choose freely. Any pair of charts in the collection must be compatible for parts of the manifold on which their domains overlap. Two charts with such compatibility are said to be $C^{\infty }$-related.

A set of charts that are $C^{\infty }$-related and whose domains cover the entire configuration space $Q$ form an atlas for $Q$. Together, the atlas and $Q$ comprise a differentiable manifold.

Example: consider the one-dimension manifold $S^1$. We defined a single chart, ($U_1,{\varphi }_1$). If we define 3 more charts, we can construct an atlas.

$U_1=x\in S^1|x_2>0,{\varphi }_1(x)=x_1$ $U_2=x\in S^1|x_2<0,{\varphi }_2(x)=x_1$ $U_3=x\in S^1|x_1>0,{\varphi }_3(x)=x_2$ $U_4=x\in S^1|x_1<0,{\varphi }_4(x)=x_2$ It is clear that together this collection covers $S^1$. We must show that they are $C^{\infty }$ related in order to show that this is an Atlas.

Checking the four pairs of composite maps shows that the intervals are smooth.

3.4.3 Connectedness and Compactness

A manifold is connect if there exists a path between any two points on the manifold.

The presence of obstacles can disconnect the free configuration space $Q_{free}$. In this case, the space is broken into a set of connected components.

There can be no solution to a path-planning problem if $q_{start}$ and $q_{goal}$ do not lie on the same connected component.

3.4.4 Not all Configuration Spaces are Manifolds

As a simple example, the closed unit square $[0,1]x[1,0]\subset {\mathbb{R}}^2$ is not a manifold, but a manifold with a boundary.

Beware!