3.1 Forward Kinematics

3.1.0

We want a function $f$ that maps joint configuration to its corresponding end-effector pose.

$r=f(q)$ $f:{\mathbb{R}}^n\to {\mathbb{R}}^n$ where $r$ is the task space and $q$ is the joint space

$q$ and $r$ are specific to a robot and a task.

$q$ is of size $n$ where $n$ is the number of Degrees of Freedomin joint space.

$r$ is of size $m$ where $m$ is the number of Degrees of Freedom in task space.

3.1.1

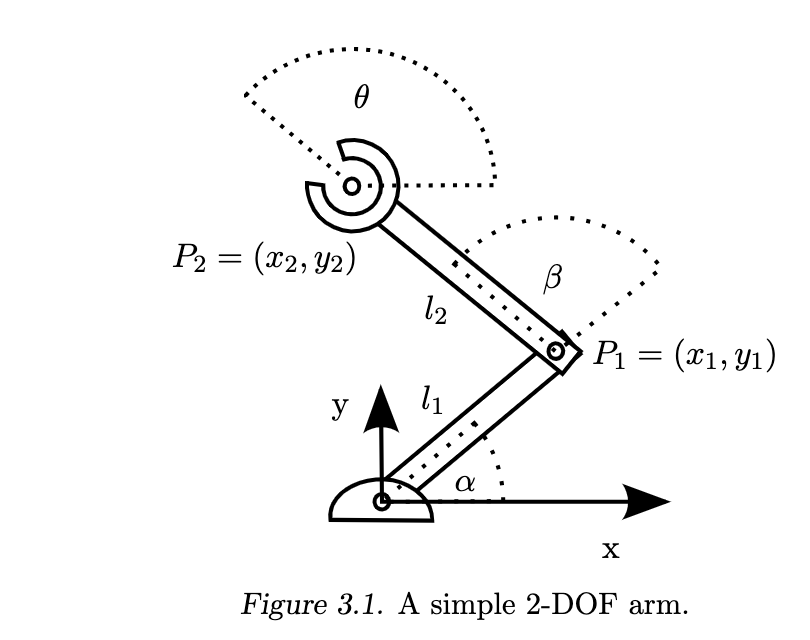Take this simple robot arm.

$q=\left[\begin{array}{c}\alpha \\ \beta \end{array}\right]$, since $l_1,l_2$ are fixed. We want $f\to \left[\begin{array}{c}x\\ y\\ \theta \end{array}\right]$ You can find $P_1=(x_1,y_1)$ using simple trig. $x_1=l_{1}cos(\alpha )$ $y_1=l_{1}sin(\alpha )$ Finding $P_2$ is very similar. $x_2=x_1+l_{2}cos(\beta )$ $y_2=y_1+l_{2}sin(\beta )$ the orientation of $P_2$ is simply $\alpha +\beta$.

Definition: Configuration Space

Each joint cannot take on arbitrary angles. For instance, $0<\alpha <\pi$, because otherwise the arm would try to go through the table it is resting on. However, $\beta$ is effectively unlimited: $-\pi <\beta <\pi$ . These constraints define Configuration Space

3.1.2 Denavit-Hartenberg notation

The above procedure is not scalable, but it effectively no different from a series of Homogenous Transformation. the DH representation is defacto standard.

In order to generically preform linear transformations up a robot arm to determine the position of an end effector, we need to establish a coordinate system for each joint. For each joint, we establish the z-axis as the axis of rotation for a revolute joint and the axis of translation for a prismatic joint. (whatever that means!)

Next, we define the x and y axes for the root joint (relatively arbitrary)- then for each subsequent joint find the line perpendicular to each z-axis (aka the common normal) and intersects both. This line becomes the x-axis for the next joint, and it points away from the previous joint. Then using the RHR you can find the y-axis for the joint.

The transformation between joints is then fully described by

1. The length $r$ of the common normal where it intersects the two z-axes of the two joints $i$ and $i-1$.
2. The angle $\alpha$ between the old and the new z-axis, measured about the common normal
3. The offset $d$ along the previous z-axis to the common normal.
4. the angle $\theta$ from the old x-axis to the new x-axis, about the previous z-axis.

You can then define a transformation and apply them in a chain a la Frames of Reference.